◆秋山 仁

PDFファイル

女王を喜ばせたパズル

1905年5月、英王立協会の会合に招かれたイギリスの数学者であるデュードニー（1857〜1930）は、ビクトリア女王を前に「仕立屋さんのパズル」を披露しました。正三角形を四つの断片に切り分け、それらを並べ替えて正方形を作れという問題です。彼は、マホガニーの正三角形を図1左のように四つの断片に切り分け、それらを真鍮しんちゅうのちょうつがいで鎖状につないだ模型を使って（図1中）、鎖の上端を固定し、他端を時計回りに回転させると正三角形（図1左）になり、反時計回りに回転させると正方形になる（図1右）様子を実演し、女王を大いに喜ばせたそうです。

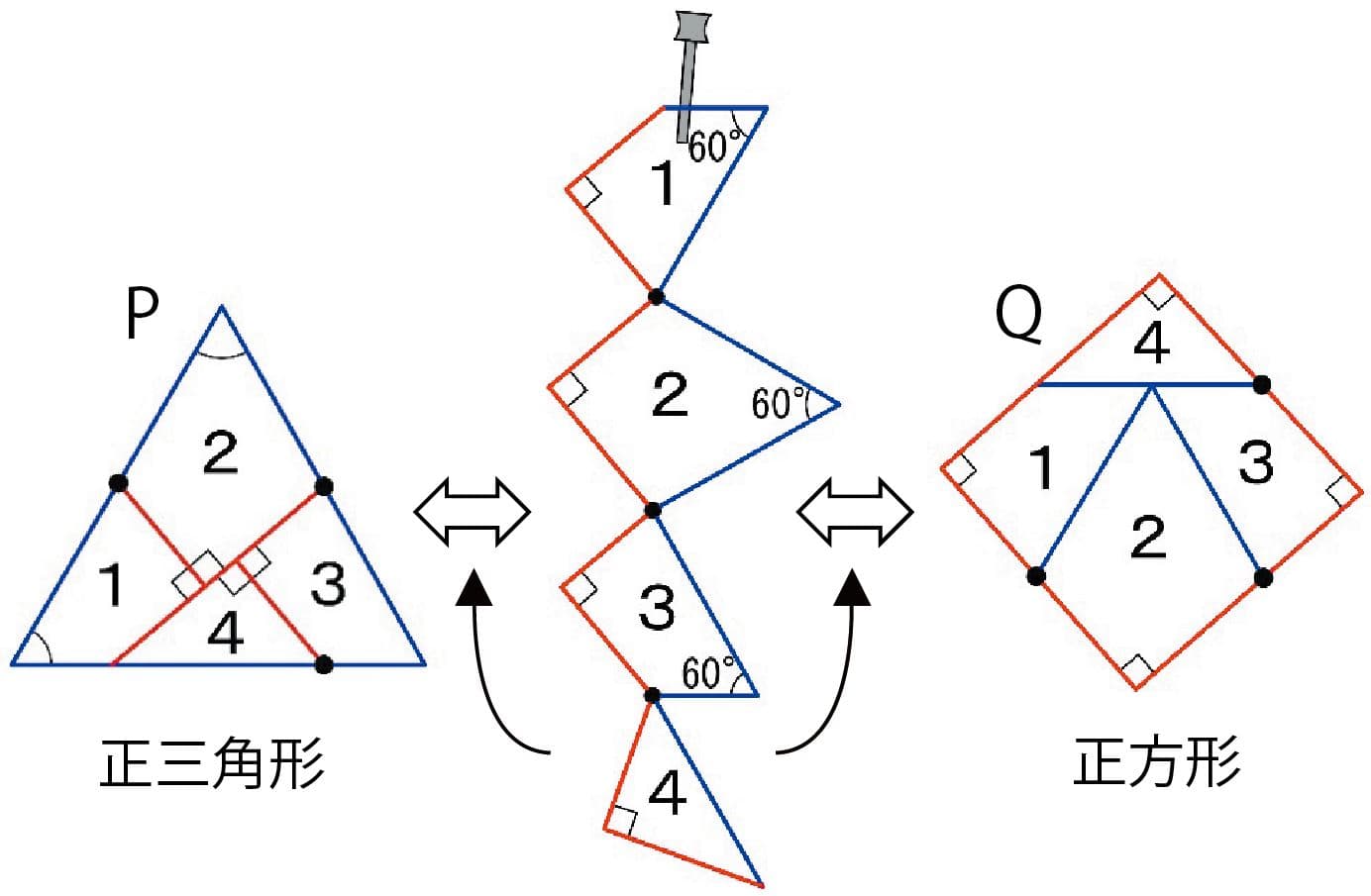
図１

このように、図形Pをいくつかの断片に切り分けて鎖状につないだ断片の端の一つを固定し、他端を左右に回転すると、図形Pまたは図形Qを得る時、PとQを変身ペアと呼ぶことにします。

長らく、正三角形Pを正方形Qに変身させる切断の仕方を見つけるために有力とされてきたのが、Pのあるタイル張りとQのあるタイル張りをうまく重ね合わせて（図2a、2b）、どのPもQのタイル張りの境界によって分割される形状が同じになるような位置を探し出し（図2c）、PをQの境界に沿って切る（図2c）という方法でした。適正重ね合わせ法と呼ばれるこの方法で、今までにいくつもの変身ペアが見つけられています。

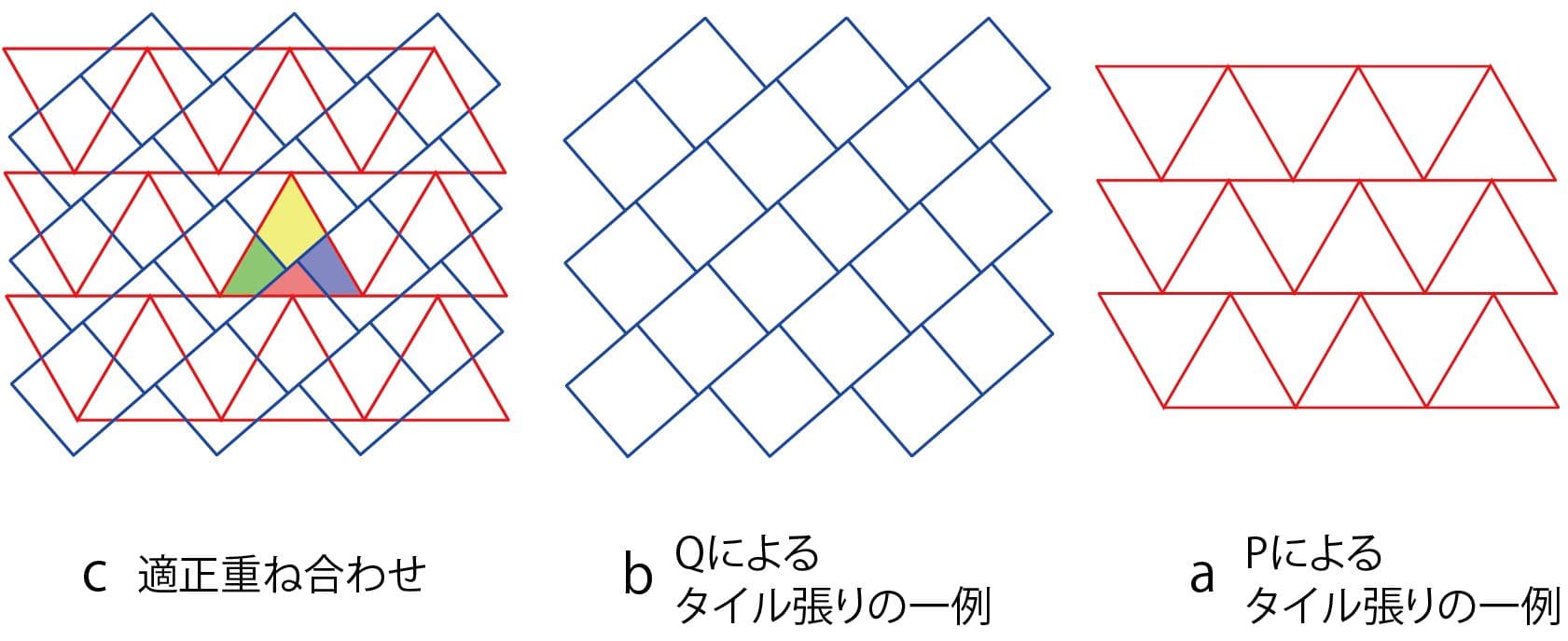
図２

変身ペアを無数に作る方法

適正重ね合わせ法よりも、簡単に、変身ペアを作る簡単な方法があるので紹介しましょう。

⑴封が閉じている封筒を１枚用意してください。

⑵封筒には、おもて面とうら面の２面があります（図３）。

図３

⑶封筒の４隅をA、B、C、Dとします。封筒のおもて面の４点A、B、C、Dに対し、図４の青線のように、どの点からどの点へも線をたどっていける経路（切断線）を描きます。

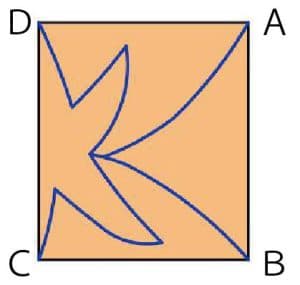
図４

⑷次に、封筒のうら面の４点A、B、C、Dに対し、図５の赤線のように、切断線を描きます。赤線に沿って、うら面だけを切り開くとエビが現れます（図8）。

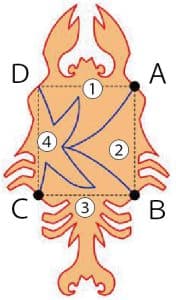
図８

⑸封筒の両面それぞれに青、赤の切断線が描けました。そこで、封筒をまず、青線だけに沿って、おもて面だけを切り開いてみましょう。すると、魚が現れます（図６）。

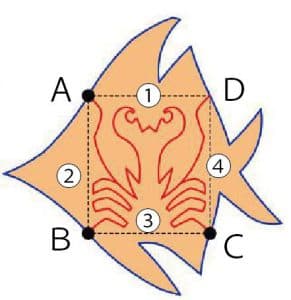
図６

⑹次に、魚を赤線に沿って４つの断片①〜④に切り分け、各点A、B、Cを共有する二つの断片のペア（①と②、②と③、③と④）をちょうつがいでつなぎ、断片の鎖を作ります（図７）。

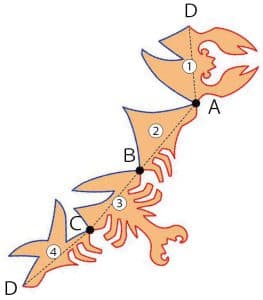
図７

⑺この鎖の上端を固定して反時計周りに回転すると魚が現れ（図6）、時計回りに回転するとエビが現れます（図８）。

⑻経路の赤線・青線の形状を変えれば、封筒から無数の変身ペアが作れます。

切り方を変えると、図９の鷹と鳩の変身ペアが作れます。鷹は、アメリカの政治家であるトーマス・ジェファーソンの発言以来、戦争の象徴とされ、鳩は平和の象徴です。鷹から鳩へ（戦争から平和へ）、願ってやまないこの頃です。

図９

平和を象徴する鳩