◆秋山 仁

PDFファイル

「多くの植物は、花粉を運んでくれるハチやチョウなどの虫を誘い込むために香りで魅力を高めます。」と、本コラムの前の執筆者・田中修先生が書いている記事を読んで、花の賢さに感心しました。

実は花のなかには、知ってか知らずか数学的な工夫を凝らしてハチやチョウなどの虫を誘い込んでいるものがあります。雪に閉じ込められた長い冬にジッと耐え〝早く、春よ来い〞と願っているのは人間だけではありません。雪の中から最初に芽を出し、花を咲かせる植物の一つにフクジュソウがあります（図１）。

図１．フクジュソウ

フクジュソウは花弁が太陽光に応じて開閉する（日光が当たると開き、日が陰ると閉じる）性質を使って日光を花の中心に集め、その熱で虫を誘引しているそうです。すなわち、フクジュソウは放物面（放物線を中心軸の回りに回転させてできる曲面）を成すように花びらが開いていて、日差しを花の内部にある一点（焦点）に集めて花の内部を暖めます。その暖を求めてハチやチョウなどの虫が集まり、花粉を運んでくれるのです。

放物面は、パラボラアンテナからわかるように、電波、光、音などを放物面に反射して固定された一点（この点を焦点といいます）に集めます（図２）。最近、太陽光を利用して料理する道具、通称ソーラークッカーが市販されていますが、これも放物面の性質を応用してつくられたものです（図３）。

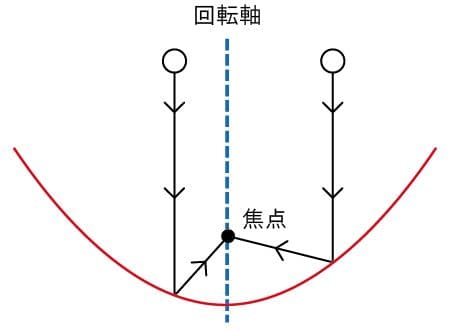
図２．放物面の焦点

図３．ソーラークッカー ©工房あまね

このように、フクジュソウは人間よりも早く放物面の性質を使って太陽光を活かしているエコの先輩なのです。

人類で最初に放物面を応用した人はおそらく古代ギリシャ時代のアルキメデスでしょう。海上に浮かぶ敵艦を焼き払うため、彼は太陽の軌道を考慮し、緻密ちみつな計画を立てました。敵艦がちょうど焦点の位置になるように、夜の間に近くの海岸に多くの鏡を放物面上に配置しました。翌日、太陽が昇ると敵艦は見事に焼き払われたのです（図４）。

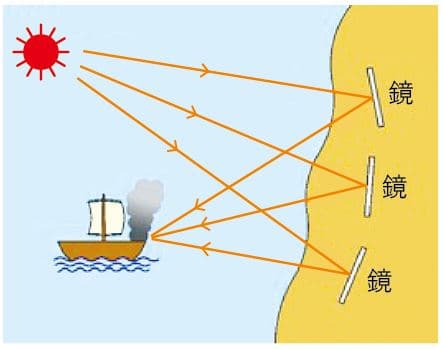
図４．放物面上に鏡を配置

放物線は円錐えんすいを平面で切った時の切り口に現れる図形の一つです（図５：黄色が楕円だえん、橙だいだい色が放物線、青が双曲線、赤が円）。仲間には楕円と双曲線があります。ちなみに円は楕円の特別な場合です。放物線は焦点が一つしかありませんが、楕円には二つあります。二つの焦点を結ぶ直線の周りに楕円を回転させて得られる曲面を楕円球といいます。ラグビーのボールのような形です。楕円球の一方の焦点の位置から、どの方向に光や電波を放っても、それは楕円球の表面で反射してもう一つの焦点に入るという性質があります（図６）。

図５．円錐を平面で切った時の切り口に現れる図形

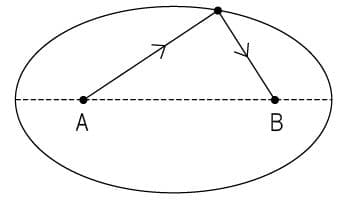
図６．楕円の焦点は二つ

この性質を応用したものに、体外衝撃波結石破砕装置があります。図７のように手前のふたのしてある容器状の装置の内側は、楕円球の下半分の形をしています。この中に、一つの焦点Ａがあります。患者さんの結石がもう一方の焦点Ｂの位置になるように設定し、医師が焦点Ａの位置から衝撃波を四方八方に発射させると、衝撃波は半楕円球の側面で反射し、結石があるＢに一斉に集まります。この結果、結石は粉々に砕け、体外に自然に排出されるのです。

図７．体外衝撃波結石破砕装置
提供：東京警察病院泌尿器科 松島常部長

円錐曲線はとても便利であることがおわかりになったと思いますが、実はこの曲線はとても混沌こんとんとした宇宙をも支配しているのです。

ご存のように惑星の軌道は楕円軌です。また、現在までに観測されている約700個の星のデータを分析すると、各軌道を持つ星の個数の比は、大体、図8のようになると報告されています。楕円軌道を描く星には、有名なハレー彗星すいせいやエンケ彗星があります。放物線軌道を描く星に土屋・木内彗星、荒井彗星などがあります。そして、双曲線軌道を描く星にオースチン彗星、レビー彗星があります。

図８．楕円型、放物線型、双曲線型の各軌道を持つ星の個数比