◆秋山 仁

PDFファイル

自然が生み出す美しいカタチ

昔、ソーセージのテレビCMで「美味なるものには音がある！」というキャッチコピーがありましたが、覚えていますか？　お湯の中でソーセージをゆでた後、ソーセージをかむと「パリッ」と音がして、その音と同時に先ほどのキャッチコピーが流されました。

今回は「美しいカタチには、それなりの理ワ由ケがある」、すなわち、形のなかで、なるほどと思える理由があるものを紹介しましょう。

ハスの葉の上の水滴は球状をしていますが、これは水滴の表面を最小にしたいという表面張力が働くことに起因しています。一定の体積を持つ立体のなかで表面積が最小になるものは球であり、ガスタンク、水道タンク、石油タンクなどに球形が多いのも同じ理由です。つまり、タンクを造る鉄などの材料を一定量にした時、貯蔵容量を最大にできる形が球なのです。

蜂の巣を切断すると、切断面に六角形が隙間なく並んでいます。これは親蜂が巣を作る時、体内から出せるミツロウの量で蜂の子が入る巣房の面積を最大にかつ隙間なく集合体を作ろうとすると、巣房は三角形でも四角形でもなく、正六角形になるからです。

ひと昔前、給食で出される牛乳パックの形はテトラパック^Ⓡとか、三角パックと呼ばれる少しへこんだ四面体でした。正四面体をどんなにうまく詰め込んでも、隙間なく詰め込むことはできません。一方、テトラパック^Ⓡと呼ばれる四面体は空間に隙間なく詰め込めるので、運搬したり、冷蔵庫に貯蔵したりする時に便利だったのです。しかし、自動販売機で牛乳パックが販売されることになった後、しばらくしてテトラパック^Ⓡはこの世からほとんど消えてしまいました。四面体にある4つのとがった頂点（角）が、販売機の中で落下する時に管に引っかかり、しばしば故障の原因になったからです。現在はほとんどが直方体の形をしたパックになっています。

生活を便利にする美しいカタチ

道路にあるマンホールのふたには、正方形のものもたまにありますが、円形が圧倒的に多いことに気付いていましたか？　これには「ふたが円形なら、どの位置にズレても決して落下しない」という安全上の秘密が隠されています。

与えられた図形をノギスで挟み込んで測った幅を「差し渡し幅」といいます。例えば、楕だ円えんを縦方向で測った時と横方向で測った時とでは、差し渡し幅aとbは異なります（図1）。

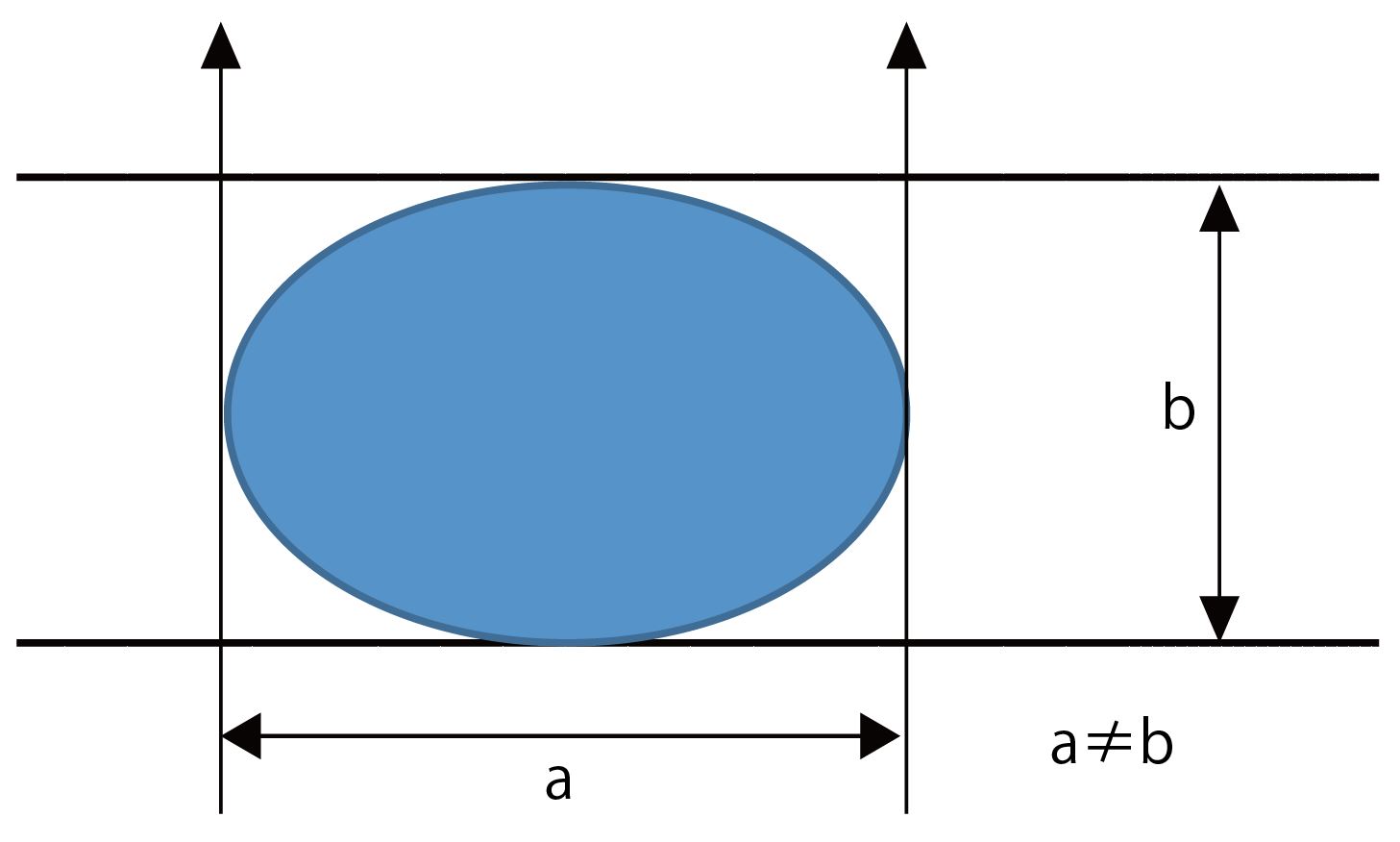
図1

どの方向から測っても、差し渡し幅がいつも同じ図形を「定幅図形」といいます。円は定幅図形なので、マンホールのふたを円にすれば、ふたがズレても落下することはありません。自動販売機に投入するコインが途中で引っかからないようにするためにも、それが定幅図形になっていることが大切です。定幅図形の仲間には円以外にも正三角形、正五角形の辺を円弧に置き換えてできるルーローの三角形、ルーローの五角形…などがあります（図2）。

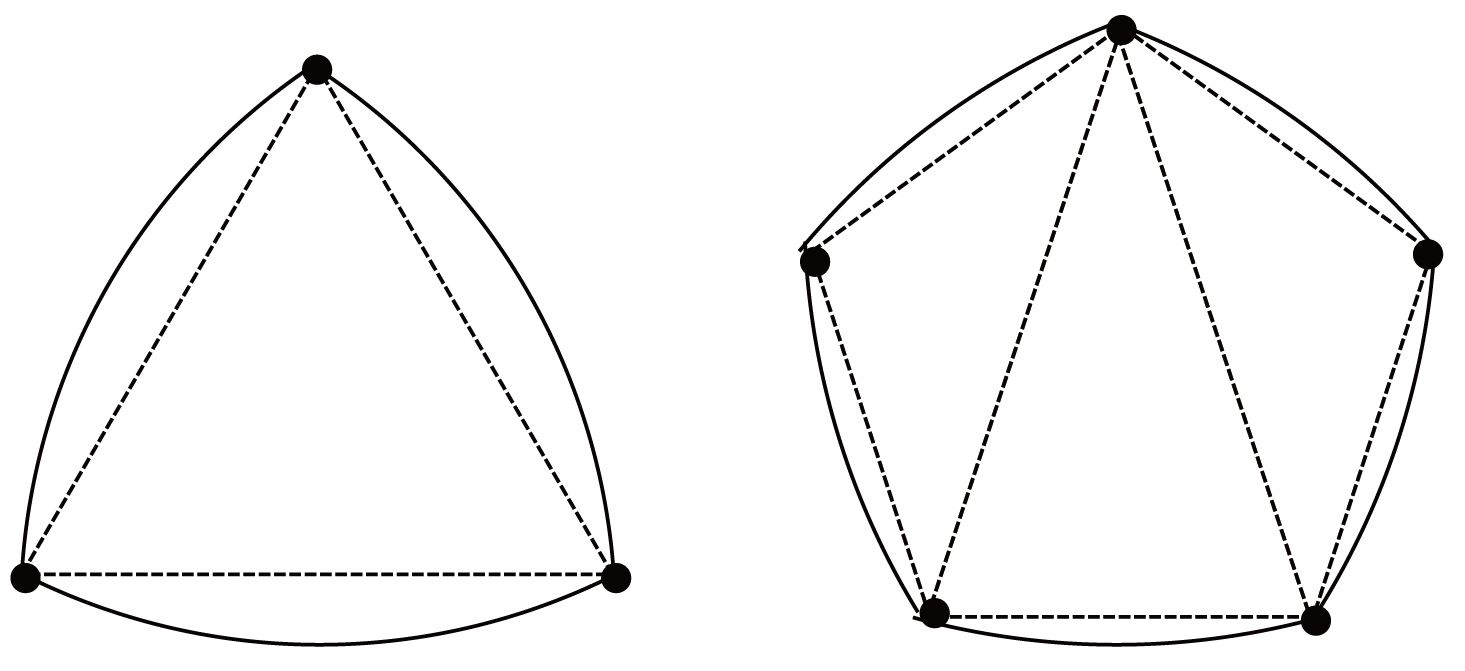
図2．ルーローの三角形とルーローの五角形

さらに、刃の形が定幅図形の回転ドリルによって、正方形の穴、正六角形の穴を開けられるというのは驚きです（図3）。実際にアメリカで特許が取られています。

図3．回転ドリルと正方形と正六角形の穴

もうお気付きの方も多いと思いますが、定幅図形は車のエンジンにもロータリーエンジンとして応用されています（図4）。ロータリーエンジンの内部では、内側の壁がトロコイド曲線（任意の曲線上を円板が滑らずに転がるときに円に固定された1点が描く軌跡）と呼ばれる繭型をし、その中でルーローの三角形の形をしたローターが回転します。その際、ルーローの三角形はトロコイド曲線に常に3点で接しながら回転できるという幾何学的な性質があります。そのような3接点により、繭型の内部は①燃料ガスの吸気室、②ガスの圧縮室および爆発室、③爆発後のガスの排気室の3つの部屋に分けることができます。ローターが1回転する間に、吸気室でエンジン内部に送り込まれたガスはローターの回転に伴って2番目の圧縮室に送られ点火され爆発し（動力化され）、さらなるローターの回転に伴い燃焼後のガスが排気室に送られエンジン外部に排出されるというサイクルをスムーズにたどることができるのです。

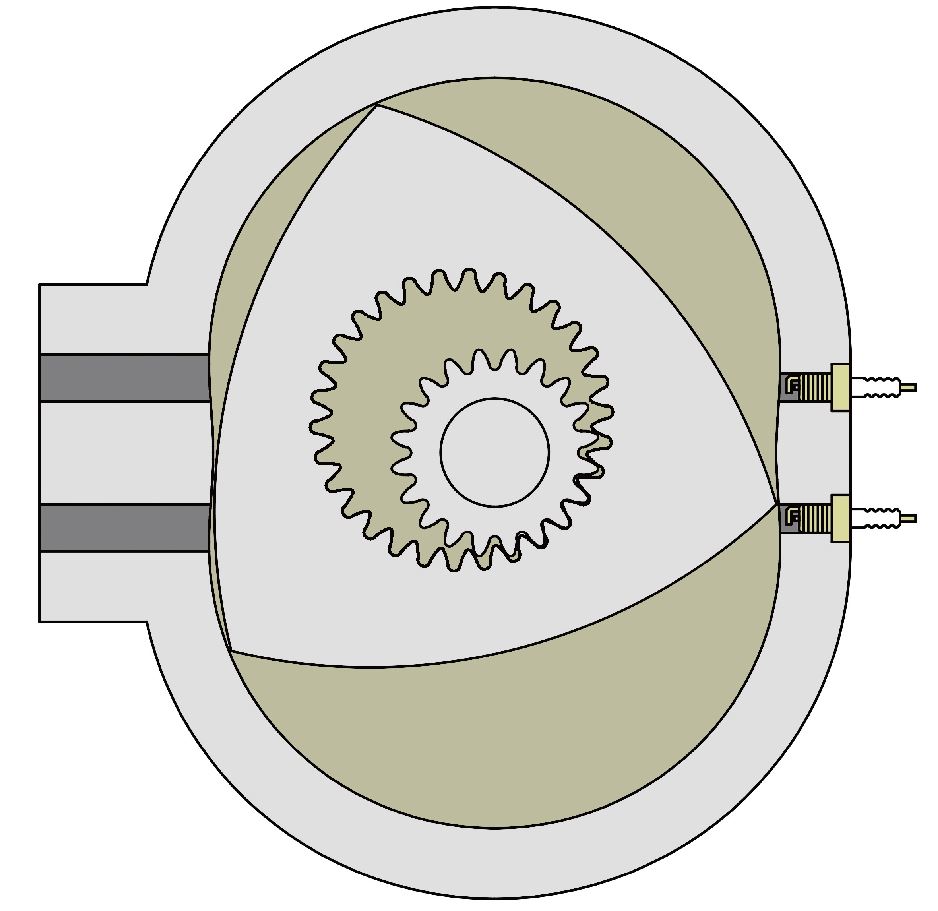
図4．ロータリーエンジン

生活で変わった形に出会ったり、その形の特性を分析したりするとそれなりの理由がわかるかもしれません。