◆秋山 仁

PDFファイル

手掛かりから理詰めで問題を解く

このところ腰痛で外に出るのがおっくうになり、チャンスとばかりに録りためていた『刑事コロンボ』を退屈しのぎに家で見ていました。サスペンスの多くは犯人が誰だかわからないままストーリーが展開され、容疑者、証拠、動機、真犯人は、作家や脚本家の思いのままに話が進められます。要するに、最終的に誰が犯人になっても良い構成になっているのです。それに対し『刑事コロンボ』シリーズは、最初に殺人のシーンを視聴者に見せるので、動かしようのない真実が視聴者にも突き付けられてしまいます。だから、作家は都合良くストーリーを展開することはできません。従ってコロンボ刑事（と視聴者）は、殺人現場に残された手掛かりから理詰めで犯人を追い詰めていくことになります。

これは誠に、数学の問題を解く時の手法に似ています。もしコロンボ刑事が数学を仕事にしていたら、素晴らしい業績を上げていたことでしょう。このシリーズのもう一つの魅力は、容疑者の肩書が政治家、弁護士、作家、建築家、音楽家、医師、科学者など多彩で、その道のプロばかりなので、彼らのすむ独特の世界を垣間見せてくれることです。「殺しの序曲」という回では、高IQ集団の社交クラブが舞台でした。コロンボ刑事は犯人とおぼしき者から、次のような有名なパズルを出題されました。

【ニセ金貨問題】

ここに金貨が入った袋が10袋ある（図1）。各袋には10枚以上の同一の金貨が入っている。そのなかの一つの袋だけにはニセ金貨だけが入っている。本物の金貨は1枚10グラムだが、ニセ金貨はそれより1グラムだけ軽い9グラムである。はかりを1回だけ使って、ニセ金貨の入っている袋を特定せよ。

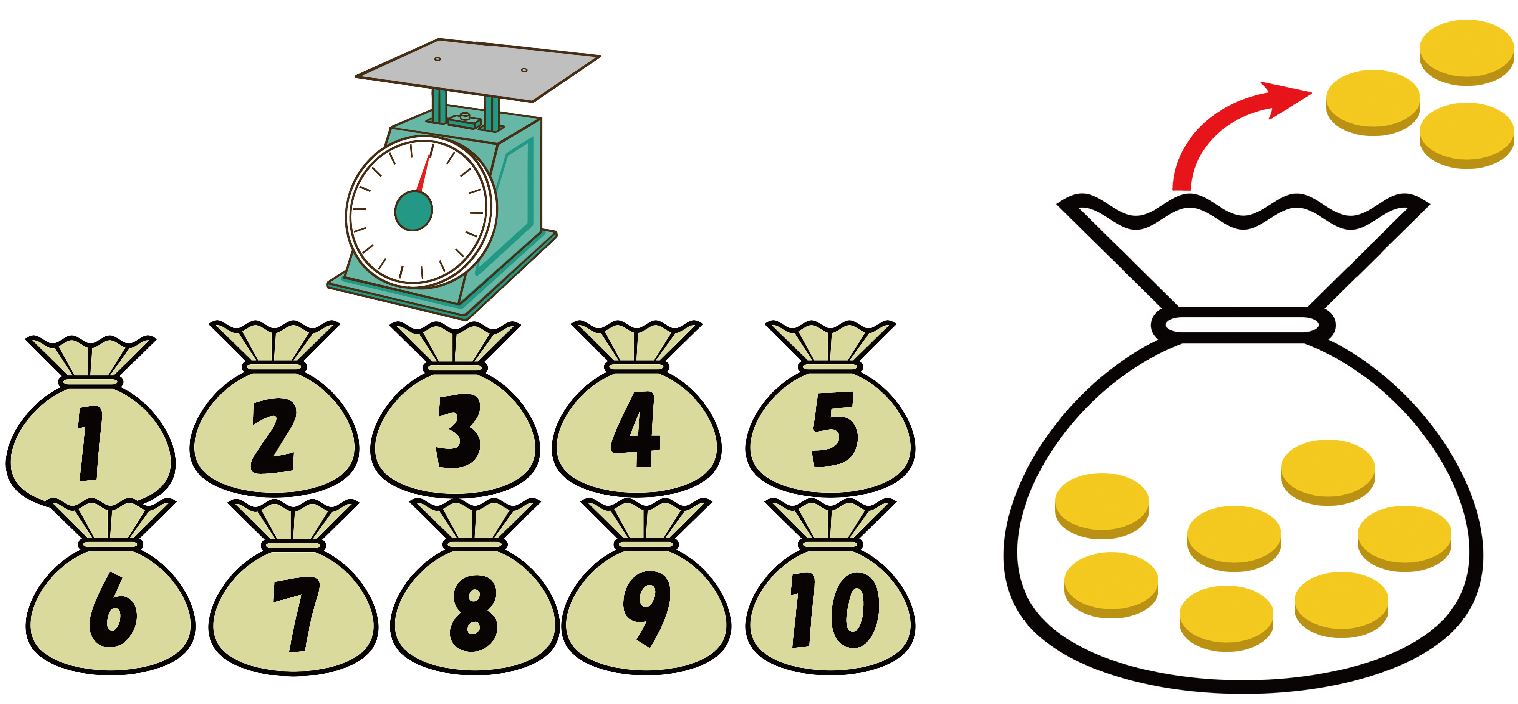
図１

「1対1対応」で鮮やかにニセ金貨問題が解ける

この問題を解く鍵は「1対1対応」という概念を巧妙に利用することです。例えば、ネット販売では商品名を入力しなくても、商品番号をクリックすれば所望の商品が届きます。これは扱う全ての商品と商品番号（数）との間に1対1の対応を付けることで、番号だけで商品を識別できるからです。

何かと何かの間に、1対1対応を付けて首尾良く解ける典型的問題に、甲子園の高校野球大会の総試合数を数える問題があります。例えば、全出場校を50校としてトーナメント（勝ち抜き戦）を行った場合、優勝校が決まるまで合計何試合するかという問題です。ただし引き分け再試合はないものとし、シード校がいくつあっても構いません。この問題では、1試合行うごとに1校が敗退することに注目しましょう。すなわち「一つの試合」と「敗退する一つの学校」の間に1対1対応を付けるのです。すると優勝校が決まるまで50－1＝49校が敗退するので、総試合数は合計49回となります。

もう一つ、1対1対応を付けると首尾良く解ける問題を紹介しましょう。3×4＝12個の錠剤が入ったシートがあります。このシートには縦、横にそれぞれ3本、2本の溝（切り分け線、図2の点線）が入っています。錠剤シートを縦や横の溝に沿ってパキッと折り、12個の錠剤を1個ずつバラバラにしたい。さて、このシートを何回パキッと折れば12個バラバラになるでしょうか？ ただし、シートを重ねて折るのは禁止とします。「溝（点線）に沿って折る」ことと「シートの断片が1個増える」ことの間に1対1対応を付けます。すると、最初は1個（3×4シート自身）だった断片が最終的に12個の断片になるので、どのように折ろうとも、バラバラにするまで12－1＝11回折らなければならないことがわかります。

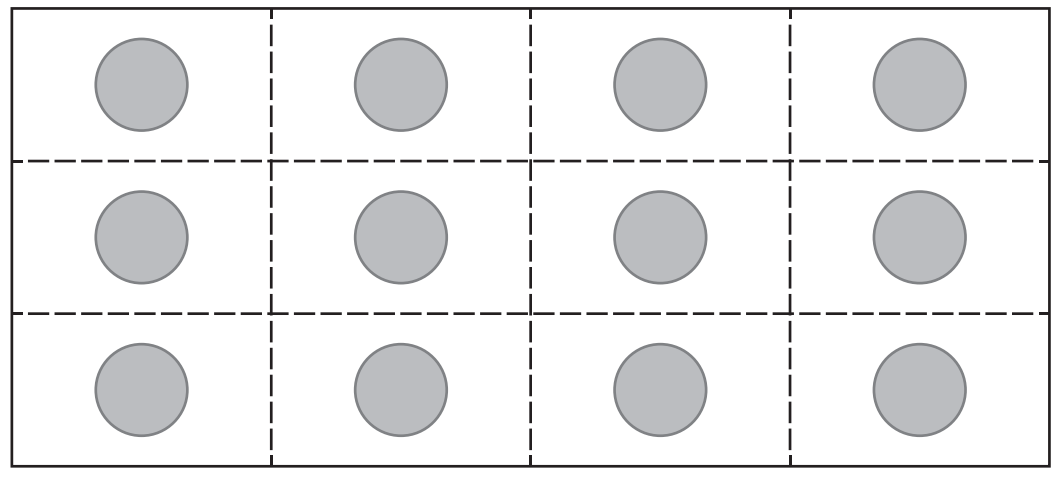
図２

さあ皆さん、1対1対応の使い方に慣れたところで、コロンボ刑事が挑戦した「ニセ金貨問題」を鮮やかに解いてみましょう。

10個の袋それぞれに1、2、…、10の番号を付ける。次に、1の袋から1枚の金貨を取り出し、2の袋から2枚の金貨を取り出し、…、10の袋から10枚の金貨を取り出し、合計1＋2＋…＋10＝55枚の金貨をはかりに載せます（図1）。全部本物の金貨なら550グラムのはずです。はかりで量った重さが550グラムより1グラム軽ければ（すなわち、549グラムならば）、袋1がニセ金貨袋であり、2グラム軽ければ袋2がニセ金貨袋であり、…、10グラム軽ければ袋10がニセ金貨袋ということになります。

一件落着、コロンボ刑事の高いIQに驚いたところ、この問題を解いたのが実は彼のカミさんだと明かしていました。私は、カミさんを一度見たいのですが、まだお目にかかれず残念です。