◆秋山 仁

PDFファイル

数学メガネをかけて不思議を発見！

この連載のタイトルは「数学メガネで周りを見れば。」ですが、それには「数学メガネで周りを観察すれば、今まで気付かなかったことに気付いたり、日常の作業が能率的になったり、時には重大な新発見につながることもある」ことを、連載を通じて読者の皆さんに伝えたいという思いを込めています。

新型コロナウイルス感染症が流行する前、あるイベントで「数学の大切さや面白さを伝える講演」を依頼されました。イベントの担当者から講演タイトルを聞かれたので、使い慣れている「数学メガネで周りを見てみると」にしました。すると何日かして、担当者から「数学メガネをいろいろ探したのですが、どこにも売っていませんでした。どこで購入できるのでしょうか？」と問い合わせがきました。生真面目な担当者には、私の比喩が通じなかったようです。トホホ。

数学メガネをかけると、不思議なことにつながる発見ができる例を紹介しましょう。

【缶の詰め込み問題】

横5センチメートル、縦8センチメートルの木箱の中には直径1センチメートルの缶が40個入っています（図1）。

さて、もう1個余計に缶を詰め込むことができるでしょうか？

多くの人は「ギッシリ詰まっているので、もうこれ以上は無理だ」と思うでしょう。しかし実は、もう1個詰め込むことができるのです（図2）。

図1では円の中心が正方形状に並ぶ配置をしています。一方、図2では円の中心が正三角形状に並ぶ配置になっています。図2のように、1個の円の周りに6個の円が囲む配置が最密であることが知られているのです。

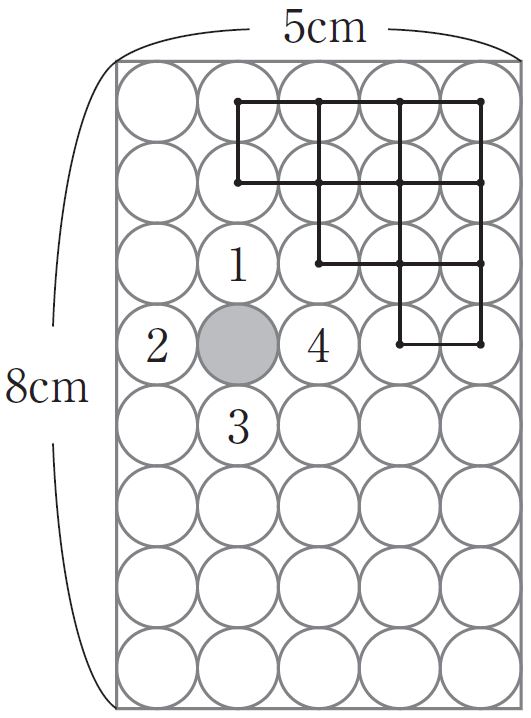図１．40個

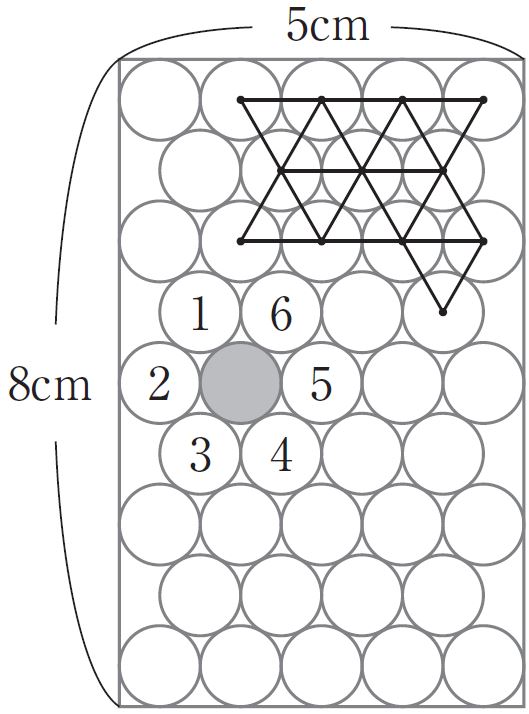図２．41個

筆者は禁煙して久しいので、最近はたばこのパッケージは見ていませんが、かつては毎日パッケージの中のたばこの配置を見ていました。20本のたばこは7本、6本、7本と3列になって詰め込まれ、たばこの中心点は正三角形状に並び、確かに最密な配列になっていました（図3）。

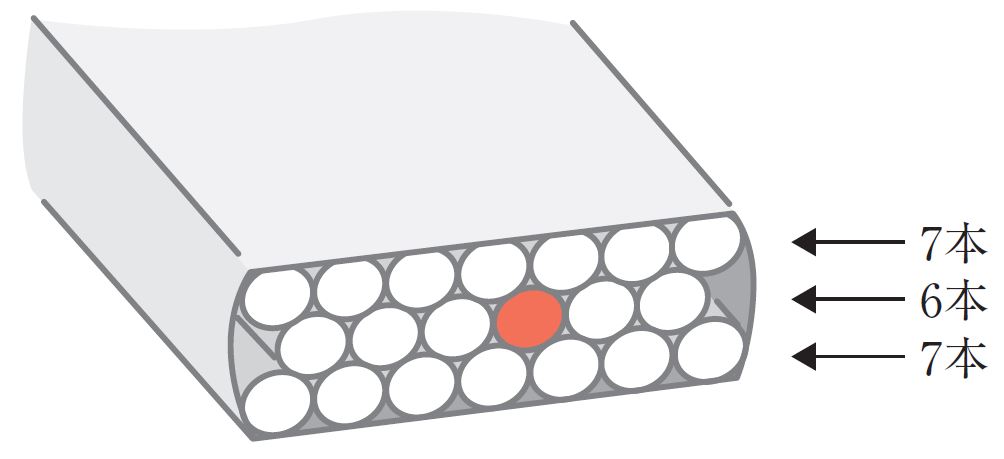
図３

工事現場に置かれているパイプや丸太も、自然と正三角形状の配置になるのです。

通信分野で応用される詰め込み問題

この問題を3次元（空間）に拡張すると、「同じ大きさの球を詰め込むための最密な配置は、何か？」という問題になります。この問題について、ドイツの天文学者ケプラーは、1611年に発行された冊子に「どの球の周りにも12個の球が囲む配置で空間を埋め尽くした場合が答えだ」と、証明を書かずに記述しました。ケプラーはザクロの種子の観察によってこのヒントを得たそうです。

ザクロの実の中にたくさん入っている種子は、球形をした小さい種子が大きくなるにつれ、互いに押し合いへし合いを始めます。その結果、最密な状態をつくり、1個の種が12個に囲まれる配置になったというのです。

すなわち図4の右のように、1個の球の周りを6個の球が取り囲み、赤点のところに上から3個を置き、黒点のところに下から3個を置くと、上下から3カ所のくぼみに球が入り込むことになります。すると、3段にわたって合計12個の球が真ん中の1個に接する配置になります（図4左）。

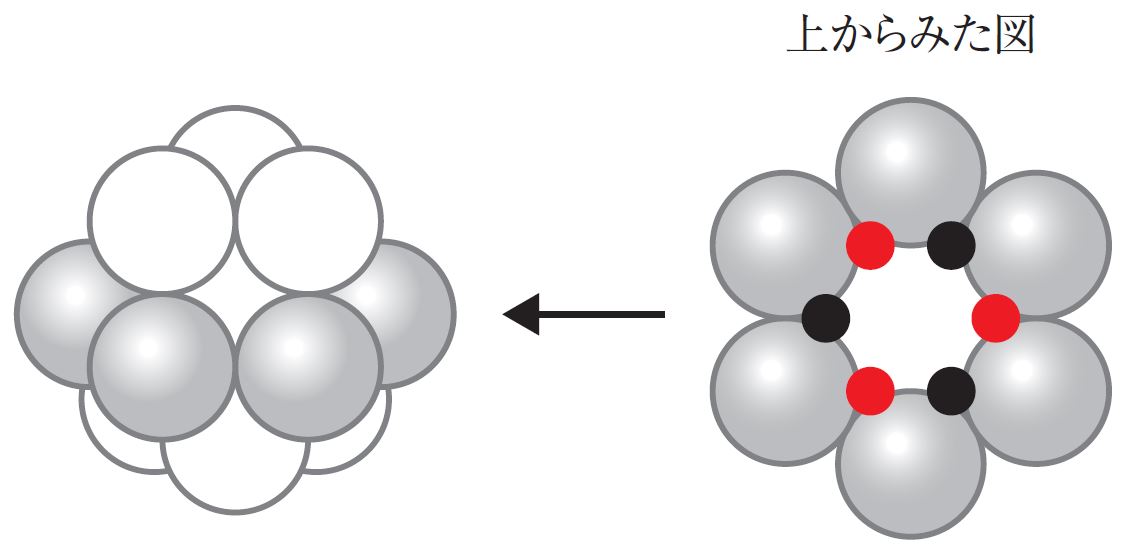
図４

〝限られた空間にできるだけたくさんのものを詰め込む〞という最密充填じゅうてん問題の応用は各分野で研究されています。

特に、通信分野では顕著です。2つ以上の信号（これを点で表します）が近くにあると、読み間違いをしてしまうことがあります。そこで、信号の誤読率を低く抑えるために信号の間隔を空けなければなりません。例えば、信号同士の間隔が最低1センチメートル必要としましょう。すると〝1辺1メートルの立方体にできるだけ多くの点を、どの2点間の距離も1センチメートル以上離して配置する〞問題になります。すなわち〝この立方体に直径1センチメートルの球をなるべく多く詰め込む〞という問題に置き換えられます。

現在は3次元どころか、もっと高い次元において球の詰め込み問題が研究され、通信工業の分野で著しい成果が上げられているのです。