MENU
三洋化成ニュース No.541
2023.11.14
2023年5月、広島で行われたサミットは各国の首脳たちに原爆の非業を実感してもらう絶好の機会となりました。米国の現職大統領で広島を訪れたのはバラク・オバマ氏が初めてだったので、とても印象に残っています。特に、彼が自分で折った折り鶴を、地元広島の2人の子どもたちに手渡したシーンは感慨深いものがありました。
言うまでもなく、折り紙は日本の伝統文化の一つです。複雑な形をした動物を、いとも簡単に折る日本人を見て、大抵の外国人はその幾何学的なセンスに驚嘆するそうです。長い間、折り紙は遊びの範疇とみられていましたが、最近になって実生活にもいろいろな応用があることが知られ、世界中で盛んに研究されています。
例えば「パラシュートをどのように折り畳んでおけば、落下途中で絡まないか」「車内に搭載されている命を守るためのエアバッグの畳み方」「回収に便利な折り畳み式のペットボトルの設計」「薬を包んだオブラートが、患者の患部に届いた時にスムーズに開いて薬を投下し、その直後に排出されやすい形に畳まれる設計」「山岳地図を頼りに登山している最中、急に雨が降っても即座に折り畳める地図」「宇宙ロケットの開閉自在な太陽光電池パネル」など、枚挙にいとまがありません。このように工学、建築学、医学などにたくさん応用される折り紙は幾何学的に研究しがいのある分野です。
さて、皆さんにも折り方の妙味を堪能していただきましょう。
コピー紙に星型の絵が描かれています(図1)。その紙を何度か折り、裁断機(またはハサミ)でたった1度の切断で、その星型を紙からスッポリと切り出すことができるでしょうか? 図2のように折れば、裁断機で1度ガチャンと切るだけで所望の星型をスッポリ切り出すことができます。

図1
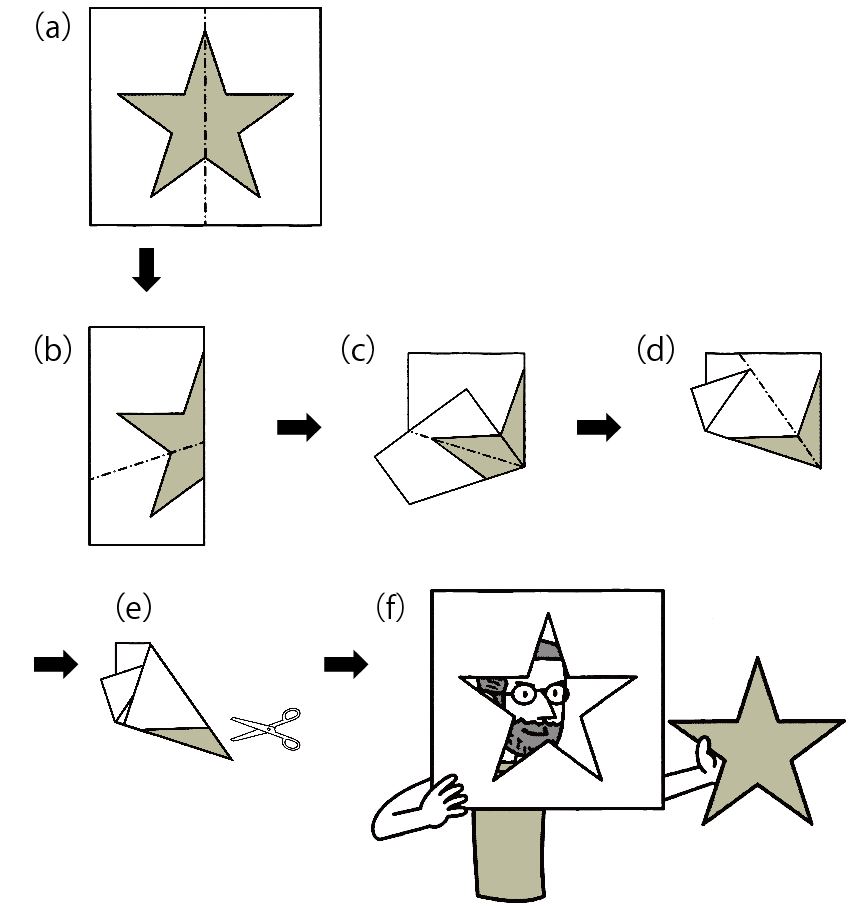
図2.一刀斬り
こういったタイプの問題は、日本でも江戸時代から楽しまれ、多くの書物、例えば『和国智恵較』でも「一刀斬りの問題」として紹介されています。
この事実を拡張して、マサチューセッツ工科大学(MIT)のエリック・ドメイン教授は次の定理を証明しました。
「紙に勝手な形をした多角形(どんな複雑な形でもよい)が描かれているとする。この時、その紙を何度か折り、それを裁断機でたった1回切断するだけで、その多角形を紙からスッポリと切り出すことができる」
この定理のすごいところは、千差万別、無数にある「どんな多角形(線分で囲まれた図形ならへこんでいても可)」でも一刀斬りが可能であることを証明した点です。
先ほど紹介した地図の畳み方で顕著なものに〝ミウラ折り〞があります。〝ミウラ折り〞の名前はこの折り方の考案者である三浦公亮博士にちなんで付けられました。図3はその折り方を示しています。実際に皆さんも折ってみて、紙の対角線の両隅を引っ張ったり、縮めたりするだけで、地図が開いたり閉じたりする様子を確認してみてください。
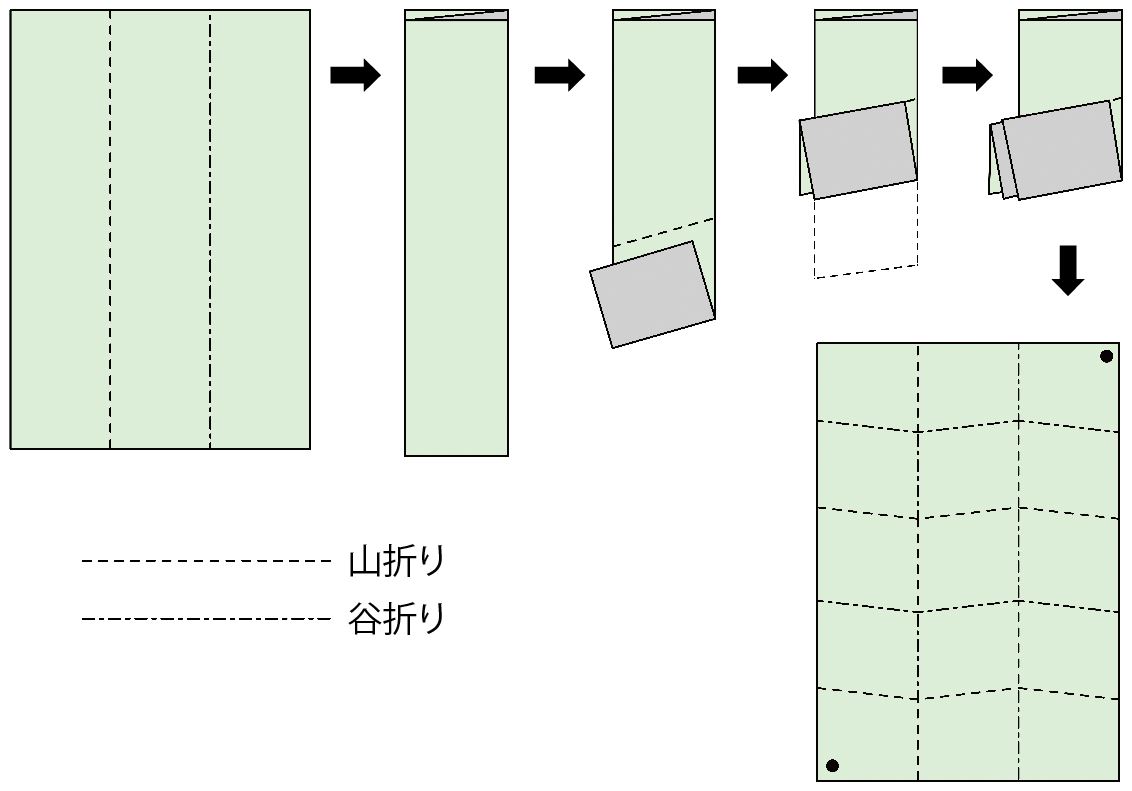
図3.ミウラ折り
幾何学の最先端の未解決問題を紹介して終わりにしましょう。
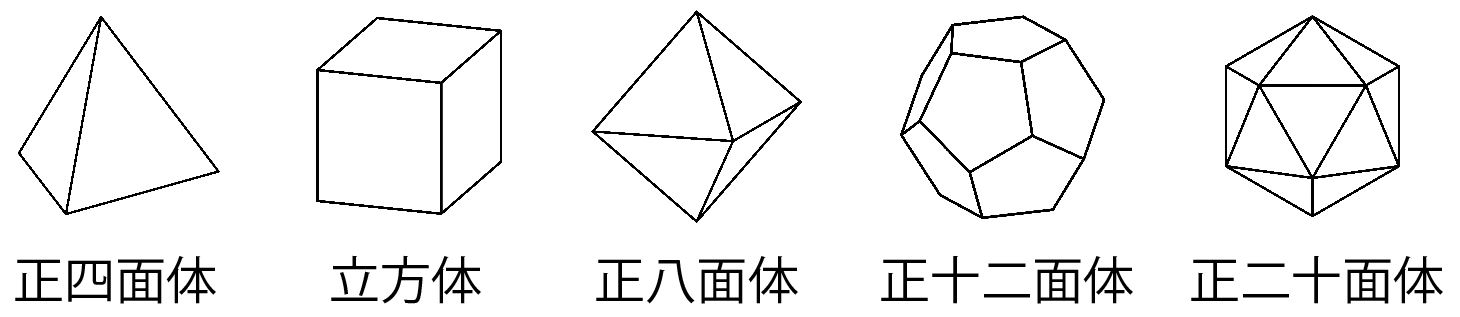
図4.5種類の正多面体
図4は5種類の正多面体の図です。そのおのおのの展開図を折り直して、四面体に折ることができるという予想を著者は7、8年前に立てました。正十二面体以外に対しては、この予想が正しいことが証明されました(図5)。(もっとも正四面体は、はじめから四面体だからこの予想が成り立つことは当たり前です)
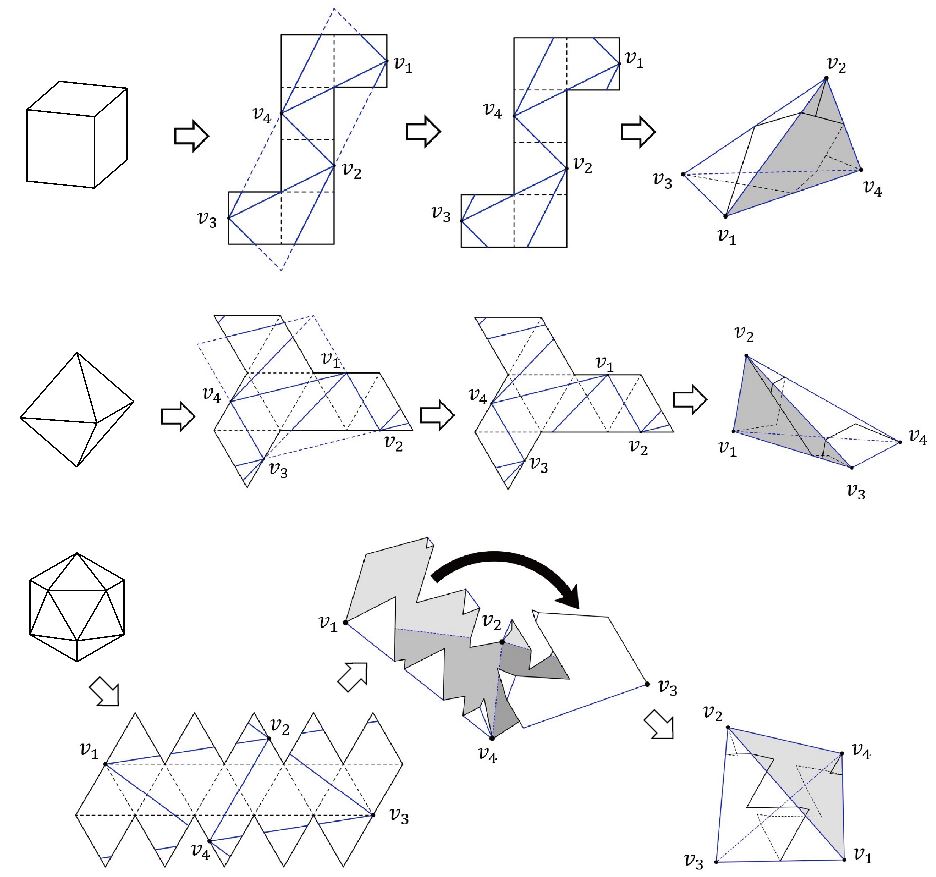
図5.立方体、正八面体、正二十面体の展開図とそれを折ってできる四面体
1946年 東京生まれ。数学者/理学博士。東京理科大学応用数学科卒業(1969年)、上智大学大学院数学科を修了後、ミシガン大学数学客員研究員、米国AT&Tベル研究所科学コンサルタント(非常勤)、日本医大助教授、東海大学開発研究所所長、科学技術庁参与、文部省教育課程審議会委員、NHKラジオ・テレビ講座講師などを経て、現在に至る。ヨーロッパ科学アカデミー会員(2007年)、日本数学会出版賞受賞(2016年)、コロンブス騎士勲章受章(2021年)。現在は東京理科大学の栄誉教授を務め、離散数学の研究と世界各地で数学啓発活動に尽力している。