三洋化成のWEB版企業広報誌

秋山 仁

PDFファイル

バーコードの読み取りミスを知らせてくれる数字

今回は、間違い（ミス）に適切に対処する知恵についてお話ししましょう。

おなじみのバーコードは、13桁の数で「国」「メーカー」「商品」などを表しています。バーコードには、読み取りミスが起きると自動的にミスを知らせてくれる「チェックディジット」と呼ばれる数字が末尾に付いています。

チェックディジットは、（左から奇数桁目の数の和）＋3×（左から偶数桁目の数の和）が、10の倍数になるように値が定められています。図1だと、23＋3×29＝110となり、確かに10の倍数になっています。バーコードは読み取りミスを知らせてくれるだけでなく、在庫管理などの大切な情報を全て登録してくれます。

図１

バーコードはミスを知らせてくれますが、ミスの修正まではしてくれません。ところが、ミスを自動的に見つけて修正してくれる超便利な理論（誤り訂正符号）が研究され、現在は随所で実用化されています。最初に考えたのは、米国のAT＆Tベル研究所のハミング博士です。1950年頃、当時のコンピューターを使って計算処理を行っている時、たびたびコンピューターがデータを読み間違えるせいで何日かかっても計算処理が終わらないことがあり、業を煮やすことがしょっちゅうだったといいます。そんな時「データの誤りを自動的に修正できるシステムがあれば便利になるだろうなぁ」と思ったことが、この分野の誕生のきっかけになったのです。

その後、衛星からのデジタル信号の誤読を防ぐという事業目的のため、1950年代から主に米国で活発に研究され、1970年代にはCDや衛星放送、GPSなど我々の身近なところでも実用化されるようになりました。以下に誤り訂正符号を応用したマジックを紹介しましょう。

うそ当てマジック

相手がうそをついても、相手の選んだ数を当てるマジックを紹介します。

カードが7枚あり、No.1〜No.4を情報カード、No.5〜No.7を検査カードと呼びます。No.5〜No.7の検査カードは相手がどのカードでうそをついたかを当てるための〝うそ発見器〞的な役割をします。

あなたがマジシャンになり、相手にはあなたにわからないように1〜15までの数を一つ選んでもらいます。

次に、図2のNo.1〜7のカードを相手に順番に見せて、それぞれのカードに相手が選んだ数が含まれているかどうかを「YES」か「NO」で答えてもらいます。ただし答えてもらう時に、相手に1回だけうそ（間違い）をついてもらうことにします。

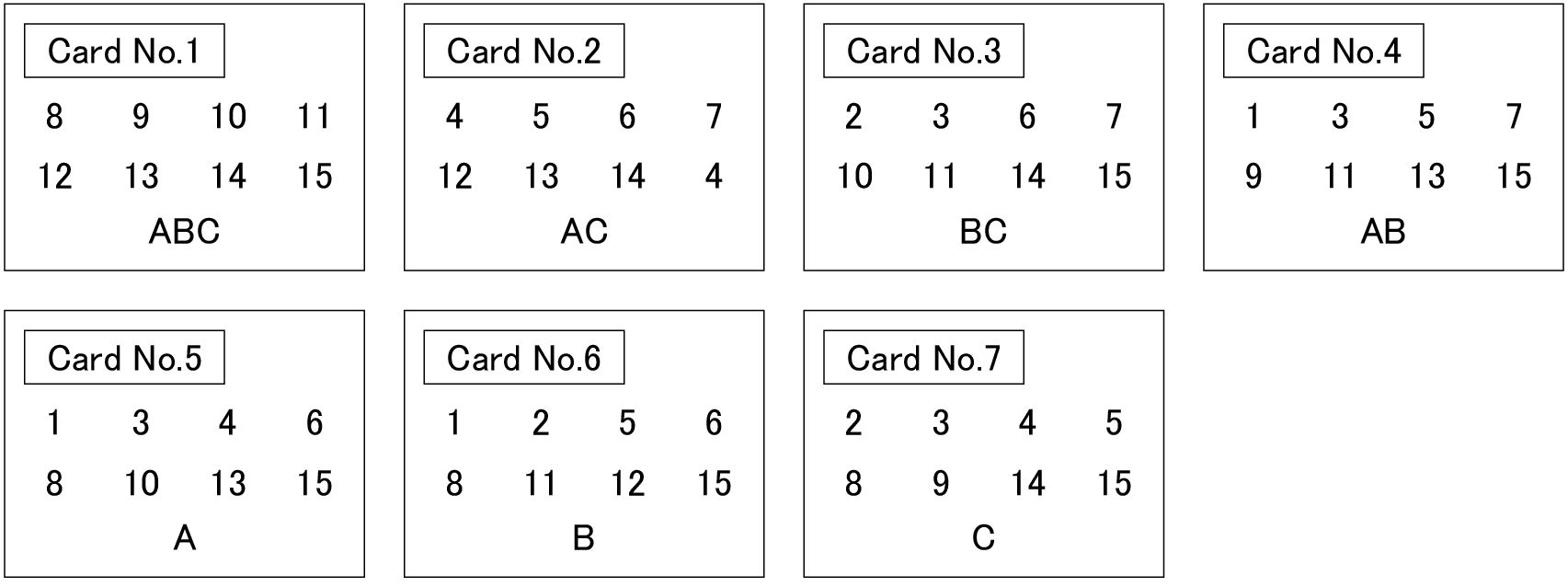
図２

例えば、相手が11という数を選んだ場合を例に取って、うその見破り方と相手の選んだ数の当て方を解説しましょう。相手が1回だけうそをついて、次のように答えたとしましょう。

Card No.1にはある（本当）、Card No.2にはない（本当）、Card No.3にはない（うそ）、Card No.4にはある（本当）、Card No.5にはない（本当）、Card No.6にはある（本当）、Card No.7にはない（本当）

マジシャンのあなたは、相手が「ある」と答えたカードを全てピックアップし（今の例では、No.1とNo.4とNo.6のカード）、それらのカードの下に書かれているA、B、Cそれぞれの出現回数を数えます。すると、A、B、Cはおのおの2、3、1回となります。

A、B、Cの中で、出現回数が奇数のアルファベットを全てピックアップします。この場合はBとCです。

カードNo.1〜No.7の中で、Step2でピックアップされたアルファベットの組み合わせが書かれているカードを探します。今の例では、BとCなので、B、Cが書かれているカードはNo.3です。そのカードで相手はうそをついたのです。すなわち、カードNo.3には、相手が選んだ数が入っているのです。よって、相手の選んだ数はカードNo.1、No.3、No.4、No.6のいずれにも含まれています。

相手の選んだ数が書かれた全てのカードの中から、検査カードは無視して、情報カードNo.1〜No.4に該当するものだけをピックアップします。この例では、カードNo.1、No.3、No.4の3枚です。
それらのカードの左上の数を足し算した数が、相手が選んだ数です。すなわち、8＋2＋1＝11となります。かくして、うそはバレてしまうのです！

己の過去の恥ずかしい過ちを全て消し去って、まともな人生に修正してくれる理論ができることを願っています。