三洋化成のWEB版企業広報誌

秋山 仁

PDFファイル

小学生の時、担任の先生に連れられて牧野富太郎博士の自宅を訪ねたことがありました。その時、牧野博士のお嬢さんから見せてもらった博士の描いた植物画の精緻せいちさに息をのんだことを覚えています。博士は植物学者として一流であったと同時に、自然の姿を鋭い観察眼をもって描画することのできる天才だったと思います。

自然のなかには、熟練した職人が技巧を凝らして描いた作品ではないかと思うような、複雑で美しい模様があります。例えば雪の結晶、シダの葉（図1）、波しぶき、フィヨルドやリアス式の海岸線、モクモクとした入道雲などなど。これらはフラクタル図形と呼ばれる図形で、その特徴は全体がそれ自身の縮小コピーで構成されている、すなわち自己相似形になっていることです。

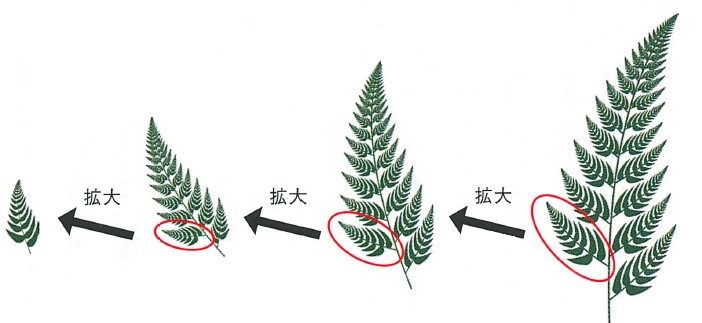
図１．フラクタル図形

見る人の視線を数学的に誘導した葛飾北斎

波といえば、葛飾北斎の「富嶽三十六景」の「神奈川沖浪裏」の絵を思い出します。この絵に描かれている大波、中波、小波はフラクタル的な雰囲気を感じさせます。北斎の絵の随所に数学的考察の跡をうかがい知ることができます。

美術評論家の中村英樹氏による（『新・北斎万華鏡』）と、この絵は「最初に、紙に2本の対角線を引く。次に紙の左下隅の点を中心とし、紙の縦の長さを半径とする4分の1の円弧を描く。このとき、富士山の頂上が右下がりの対角線と円弧の交点になっている。……」などといった具合に、構図を幾何学的に構築して描かれた作品だそうです（図2）。その結果「小舟を漕ぐ人たちが大波に飲まれてしまうのではないかとハラハラしながら大波の行く方を追って行くと、後方に小さく描かれた富士山頂が自然にあなたの視線に飛び込んでくる」という、まさに天才的手法が施されていると、中村氏は指摘しています。

図2．「富嶽三十六景　神奈川沖浪裏」

鑑賞者の視線を数学的に誘導するという天才技を持つ北斎は、日本よりむしろ海外で評価が高いようです。例えば1999年にアメリカの雑誌『LIFE』のアンケート「この1000年間で最も重要な業績を残した世界の人物100人」のなかに、唯一ランクインした日本人は北斎だったのです。

幾何学的に絵を描いたダ・ヴィンチ

西洋で数学と芸術が融合したのはルネサンスの時代でした。絵画の歴史を見ると、大雑把にいってルネサンスの前と後では、絵を見た時の感じが大きく違っています。

それは、ルネサンス期に入って絵画に遠近法が導入されたからです。それ以前の絵画は遠近法が導入されていませんでした。遠近法は、人間がものを見る時に、遠くにあるものほど小さく見えるので、見えている姿そのままに描くという画法です。すなわち、2次元のキャンパスに描いたものが自然に3次元的に見えるようにする、いわばイリュージョン的手法です。

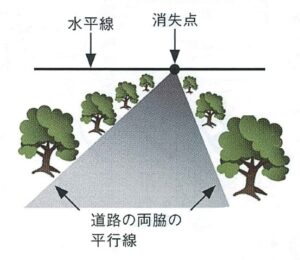
図3．遠近法による作図の仕方

どのようにするかというと、まず紙に目の高さを示す水平線を描き、さらにその水平線上の任意のところに「消失点」を取ります。消失点とは、空間の中の目線に平行な二本の線が遠くに行くほど近付いていくように見え、ついに交差する点のこと。そして、実際の風景では目線と平行な関係にあって交わるはずのない線分を、全て消失点で交わるように描きます。そうすることで絵に奥行きが出てくるのです。例えば、図3のような並木道を描くとしましょう。まず、水平線と消失点を画面上に取り、次に道路の両脇の平行線が消失点で交わるように描きます。

遠近法を幾何学的に精密に探求した1人が、レオナルド・ダ・ヴィンチです。例えばダ・ヴィンチの作品「最後の晩餐」の絵の中では、実際には交わることがないはずの天井、壁、床の平行な直線が、キリストの頭の辺りで1点（消失点）に集まるように描かれています。

図4．消失点・平行線の入った「最後の晩餐」

「科学なしに（建築や絵画などといった）実践にふける者は、舵や羅針盤なしで船を操ろうとする船乗りのようなものだ」とダ・ヴィンチは述べています。数学こそが科学の根底を支えていると考えていた彼は、絵画の画法や建築などの美的作業の基礎に数学を据えました。そして「学生たちよ、まず数学を学びなさい」と、建築や絵画を志す若者にアドバイスしていたそうです。